Comment prévenir les difficultés en algèbre au secondaire?
Si vous avez eu l’occasion d’enseigner l’algèbre à des élèves du secondaire, vous avez sûrement observé leurs difficultés à s’approprier les notions algébriques. Cette difficulté, persistante dans le temps, a fait l’objet de nombreuses études, mais des questions importantes restent encore sans réponse. Deux chercheuses de l’Université du Québec en Outaouais (UQO), soit Elena Polotskaia et Nathalie Anwandter, et une chercheuse de l’Université McGill, soit Annie Savard, ont réalisé une synthèse approfondie des recherches sur le sujet, l’idée étant d’identifier les pratiques d’enseignement des mathématiques au primaire et au préscolaire favorables à la prévention des difficultés en algèbre des élèves du secondaire.

Source de l’image : Shutterstock
La recherche menée par Polotskaia, Anwandter et Savard a été financée par le Fonds de recherche du Québec – Société et culture (FRQSC) et le ministère de l’Éducation et de l’Enseignement supérieur (MEES).
Entre l’arithmétique et l’algèbre
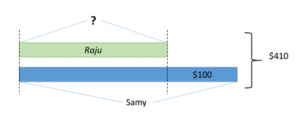
Les recherches attribuent en grande partie la difficulté à apprendre l’algèbre au secondaire à la rupture entre l’arithmétique du primaire et l’algèbre du secondaire (Kieran, 1989; Bednarz et Janvier, 1993). En arithmétique, pour résoudre un problème, les élèves du primaire s’appuient souvent sur les connaissances des nombres et des opérations, alors que les connaissances associées à la pensée algébrique reposent sur les structures et les relations entre les quantités. Pour mieux comprendre la situation, il suffit de demander à des élèves du primaire de résoudre des problèmes mathématiques (Figure 1). Un grand nombre d’élèves vont dire qu’ils « ne comprennent rien, car il n’y a pas de nombres dans ce problème ». Or, il serait possible pour ces élèves de proposer une séquence d’opérations sans nécessairement faire de calculs.
Figure 1 – Tâche de résolution de problèmes
Source : Site Web d’Elena Polotskaia
Ce que la recherche suggère
Les travaux de recherche consultés suggèrent que l’introduction de la pensée algébrique au primaire prépare bien les élèves à l’apprentissage des notions d’algèbre (Malara et Navarra, 2018), ne perturbe pas l’apprentissage de l’arithmétique (Blanton et al., 2015) et même renforce la réussite en résolution de problèmes d’arithmétique (Polotskaia et Savard, 2018).
Dans leur étude, Polotskaia, Anwandter et Savard suggèrent que les jeunes élèves ont le potentiel de développer leur pensée algébrique, mais que ce potentiel n’est pas exploité par l’enseignement traditionnel. Les très jeunes élèves ainsi que les élèves identifiés comme « ayant de difficultés en mathématiques » peuvent aussi profiter pleinement de l’enseignement orienté vers le développement de la pensée algébrique (Lee, 2006; Lüken, 2018; Warren, 2016).
L’introduction de la pensée algébrique au primaire et au préscolaire requiert une formation spécifique de la part du personnel enseignant (Malara et Navarra, 2018). Ainsi, Polotskaia et son équipe ont développé le guide Pensée algébrique précoce (version en anglais : Early algebraic thinking) destiné aux enseignants du primaire, aux orthopédagogues et aux conseillers pédagogiques. Ce guide propose neuf recommandations qui visent à apporter des changements souhaitables dans l’enseignement des mathématiques au primaire et au préscolaire. Ces recommandations visent aussi à prévenir la rupture arithmétique-algèbre et, ainsi, les nombreuses difficultés des élèves du secondaire. Le guide explique entre autres les composantes de la pensée algébrique à développer chez les élèves et présente des exemples d’activités à vivre en classe, lesquelles sont inspirées de différentes recherches consultées lors de l’étude effectuée par Polotskaia, Anwandter et Savard. En plus de la Tâche de résolution de problèmes (Figure 1), s’y trouvent entre autres les activités suivantes : Généralisation de motifs (Figure 2), Modélisation (Figure 3) et Équation imagée (Figure 4).
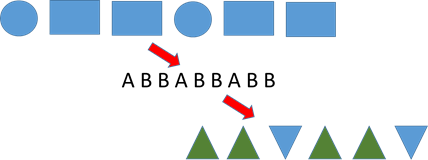
Figure 2 – Généralisation de motifs
Source : Site Web d’Elena Polotskaia
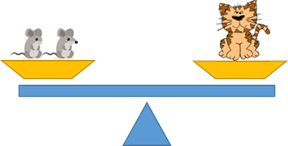
Figure 3 – Modélisation : comparaison de poids des objets
Source : Site Web d’Elena Polotskaia
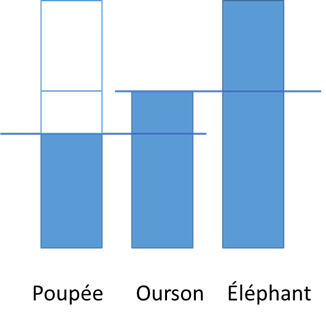
Figure 4 – Équation imagée
Source : Site Web d’Elena Polotskaia
Polotskaia, Anwandter et Savard croient que la réussite en mathématique au secondaire est accessible à tous les élèves. Elles croient aussi que leur travail peut contribuer à cette réussite, notamment grâce aux idées, aux exemples d’activités et aux perspectives d’amélioration de l’enseignement des mathématiques qu’elles proposent.
Références
Bednarz, N. et Janvier, B. (1993). The arithmetic-algebra transition in problem solving: Continuities and discontinuities. Dans Proceedings of the 15th Annual Meeting of the International Group for the Psychology of Mathematics Education (North American chapter PME-NA) (vol. 2, p. 19-25). Asilomar, California.
Blanton, M. L., Stephens, A., Knuth, E. J., Gardiner, A. M., Isler, I. et Jee-Seon, K. (2015). The Development of Children’s Algebraic Thinking: The Impact of a Comprehensive Early Algebra Intervention in Third Grade. Journal for Research in Mathematics Education, 46(1), 39-87. http://www.nctm.org/publications/article.aspx?id=43626
Kieran, C. (1989). The early learning of algebra: A structural perspective. Dans S. Wagner et C. Kieran (dir.), Research issues in the learning and teaching of algebra (p. 33-56). Reston, VA : Lawrence Erlbaum Associates. http://scholar.google.com/scholar?hl=en&btnG=Search&q=intitle:The+Early+Learning+of+Algebra:A+Structural+Perspective#0
Lee, J.-E. (2006). Teaching Algebraic Expressions to Young Students: The Three-day Journey of “a + 2”. School Science and Mathematics, 106(2), 98-104. https://doi.org/10.1111/j.1949-8594.2006.tb18139.x
Lüken, M. M. et Kampmann, R. (2018). The Influence of Fostering Children’s Patterning Abilities on Their Arithmetic Skills in Grade 1. Dans I. Elia, J. T. Mulligan, A. Anderson, A. Baccaglini-Frank et C. Benz (dir.), Contemporary Research and Perspectives on Early Childhood Mathematics Education (ICME-13 Mo, p. 55–66). Springer International Publishing AG. https://doi.org/10.1007/978-3-319-73432-3_4
Malara, N. A. et Navarra, G. (2018). New Words and Concepts for Early Algebra Teaching: Sharing with Teachers Epistemological Issues in Early Algebra to Develop Students’ Early Algebraic Thinking. Dans C. Kieran (dir.), Teaching and Learning Algebraic Thinking with 5- to 12-Year-Olds (ICME-13 Mo, p. 51–77). https://doi.org/10.1007/978-3-319-68351-5_3
Polotskaia, E. et Savard, A. (2018). Using the Relational Paradigm: effects on pupils’ reasoning in solving additive word problems. Research in Mathematics Education, 20(1), 70-90. https://doi.org/10.1080/14794802.2018.1442740
Warren, E. (2016). The development of algebraic thinking among students aged from 5‑14 years. Dans A. Gutierrez & P. Boero (dir.), The Second Handbook of Research on the Psychology of Mathematics Education: The Journey Continues (p. 74-84).



Articles similaires
Wikipédia : le type de contribution comme gage de qualité
Le style de collaboration à la rédaction d’articles sur Wikipédia a un effet direct sur la qualité de ceux-ci.
Voir l’articleWikipédia dans la classe
L’encyclopédie libre Wikipédia fait partie des outils pouvant avoir une visée pédagogique.
Voir l’articleLa voie de la réussite, la voix des étudiants
Les attitudes et les comportements scolaires sur lesquels s’appuient ces deux grands concepts sont nommés par les étudiants eux-mêmes.
Voir l’articleCommentaires et évaluations
Contribuez à l’appréciation collective