Faciliter les transitions scolaires en mathématiques à l’aide d’une communauté interordres

Source de l’image: ShutterStock

Assurer une continuité dans la formation en mathématiques entre les différents ordres représente un véritable défi. Y répondre contribuerait à la réussite des élèves. Cependant, la structure cloisonnée du système scolaire ne permet pas de garantir la continuité voulue. Si des enseignants de différents ordres se côtoyaient et dialoguaient ensemble, le fossé se réduirait.

Dans le cadre du projet ARIM, Corriveau et ses collaborateurs ont étudié quatre communautés interordres, chacune d’elles rassemblant des conseillers pédagogiques et des enseignants du primaire, du secondaire et du collégial, de sorte à trouver des pratiques qui facilitent les transitions. D’une part, les chercheurs ont souligné les tensions, lors des transitions, identifiées par les communautés. D’autre part, ils ont proposé des conditions favorables à la création d’une communauté pour l’étude des transitions scolaires en mathématiques.

Tensions lors des transitions scolaires

Suivant les multiples rencontres des quatre communautés interordres, sur plus de 340 heures d’échanges entre 77 professionnels, dont 65 enseignants en mathématiques et 10 conseillers pédagogiques, des résultats font ressortir certains constats. En voici un résumé en trois points.

1.Une volonté institutionnelle nécessaire

Bien que les institutions reconnaissent le problème des transitions, cette reconnaissance a peu de répercussions directes dans les classes. Des libérations et la mise en place de ressources permettant aux conseillers pédagogiques et aux enseignants des différents ordres de se rencontrer et d’échanger à propos de leurs pratiques seraient donc nécessaires. Ces mesures les aideraient à discuter de leurs préoccupations concernant les transitions scolaires.

2. Des manières de faire propres à chaque ordre d’enseignement

En ce qui concerne les mathématiques, les transitions entre les différents ordres d’enseignement indiquent un passage entre différentes cultures mathématiques. Uniformiser les manières de faire les mathématiques n’est ni possible ni souhaitable. Cette mesure appauvrirait la formation. À l’inverse, une concertation entre des enseignants des deux ordres où ils expliciteraient leur situation respective serait favorable.

Un tel dialogue devrait être accompagnée par des personnes qui ont développé une sensibilité au fait que les mathématiques sont culturellement situées. Elles éviteraient des échanges asymétriques et recentreraient les échanges autour de l’explicitation des situations respectives.

3.Un processus de rapprochement et des pratiques renouvelées

Une communauté interordres est susceptible de faciliter le processus de transitions. Plusieurs nouvelles pratiques ont émergé de ce type de collaboration. Elles traduisent une volonté de mieux comprendre ce qui se fait en mathématiques à chacun des ordres d’enseignement.

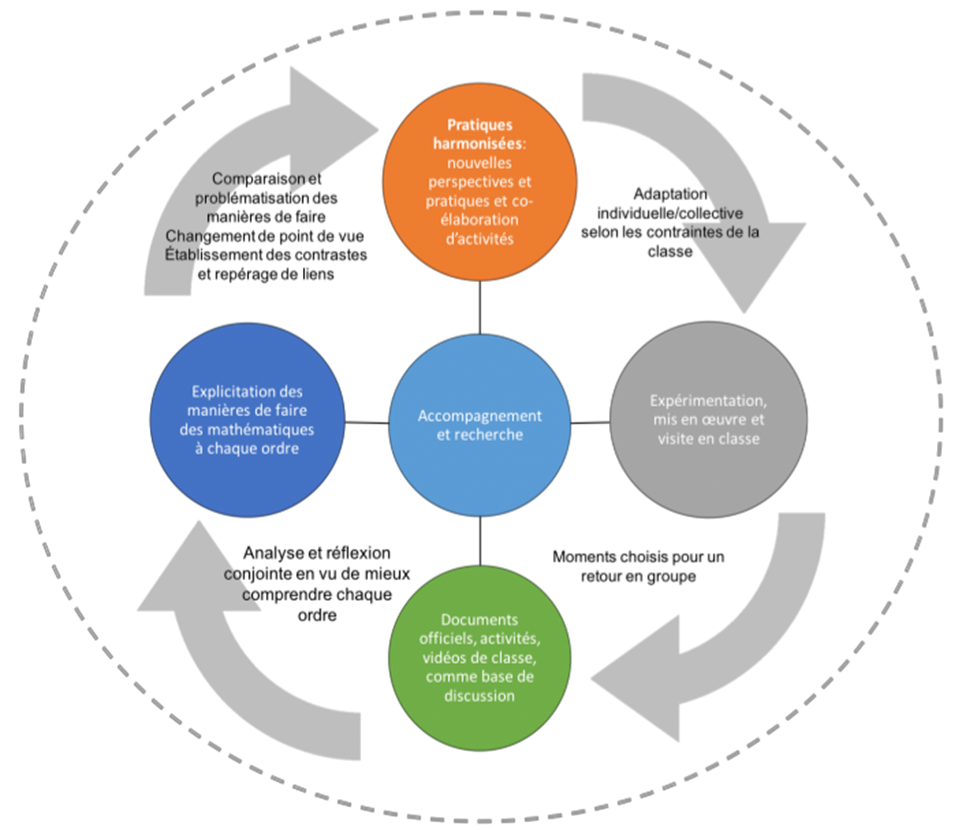
La figure suivante montre comment des discussions et des réflexions en collaboration suivent des expérimentations et raffinent à leur tour la compréhension de chacun des ordres. Le cycle se répète et fait apparaître d’autres enjeux : il devient un cercle vertueux (Corriveau et al., 2017).

Figure 1. – Processus de rapprochement interordres.

Conditions favorables à une communauté interordres

La mise sur pied d’une communauté interordres doit réunir des conditions favorables. En voici quelques-unes.

• Un climat de confiance qui soutient la prise de risques, le partage de pratiques et de connaissances, ce qui demande un temps d’apprivoisement.
• Une profondeur des discussions 
• qui encourage les idées contraires et la négociation. Avoir une ou plusieurs tierces personnes qui accompagnent aide d’ailleurs à nourrir et approfondir les réflexions.
• Une participation démocratique qui invite à établir des balises renforçant le travail collaboratif. Elle promeut aussi une certaine souplesse et des marges de manœuvre pour les gens qui participent (p. ex. un droit de regard sur les objectifs poursuivis).
• Un partage du leadership avec des membres qui acceptent de prendre des risques, de « livrer » leurs pratiques et d’intégrer les changements induits par la collaboration interordres.

Somme toute, les participants au projet ARIM ont identifié ensemble des obstacles aux transitions interordres en mathématiques. Grâce à des conditions favorables à la collaboration, ils ont également réfléchi sur des pratiques pour faciliter les transitions des élèves et, donc, leur réussite en mathématiques. Ceci, afin que les élèves soient moins à risque de vivre une situation comme celle de Mathieu.

Référence

Corriveau, C., Breuleux, A., Kobiela, M. et Oliveira, I. (2017). Projet ARIM [Actions et rapprochements interordres en mathématiques] : processus de rapprochement des pratiques d’enseignement de mathématiques pour favoriser un passage plus harmonieux pour les élèves lors de transitions scolaires (projet de recherche-action n^o 2017-PO-202613). http://www.frqsc.gouv.qc.ca/documents/11326/3897244/C.Coriveau_rapport_Projet-ARIM_PRS_2016-2017.pdf/2faf7bf7-f443-4e3d-a196-45fbd6eb40b2

[1] Nom fictif

[2] Projet ARIM : Processus de rapprochement des pratiques d’enseignement des mathématiques pour favoriser un passage plus harmonieux pour les élèves lors de transitions scolaires